背景

従来から様々な科学分野における研究は、対象となる（一般に動的な）現象の観察を通して、数理モデルを用いた表現による一般化と解析を繰り返すことで進展してきました。一方近年では、飛躍的な計測技術・情報インフラの発展を背景に、観測／計測データを用いた、データ駆動によるアプローチが重要な課題として認識されるようになっています。実際、マテリアルズ・インフォマティクスなどのように、機械学習等を用いた（静的な特性の）予測（例えば、材料の組成探索の場合は物性の予測）に基づき科学的発見、または工学的成果が多数報告される分野も出てきており注目されています。しかし一方で、（静的な特性の）予測に基づく方法ではなく、データからの直接的な現象の理解に基づく科学的知見の抽出という観点では、方法論自体の確立も不十分であるというのが現状であり今後の発展が期待される領域です。ここで、直接的な現象の理解とは、（動的な）現象を表現する数理モデル自体や、その一部、あるいは縮約モデルの獲得、またはそれに付随する物理法則（原理的メカニズム）等と直接リンクする情報の抽出を指します。このような方法論の発展を困難にする主な要因としては、一般に常/偏微分方程式等で数理的に表現される（動的な）現象に関する知識を、直接的にデータから抽出し利用可能な統計的枠組みや計算方法が確立されていない点にあります。

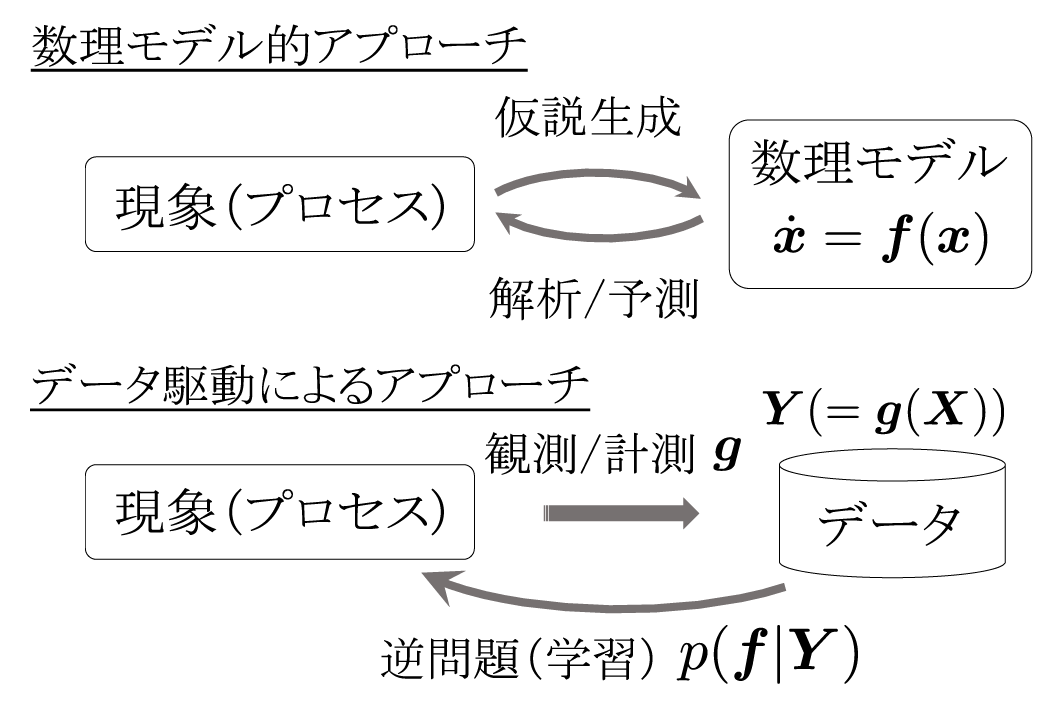
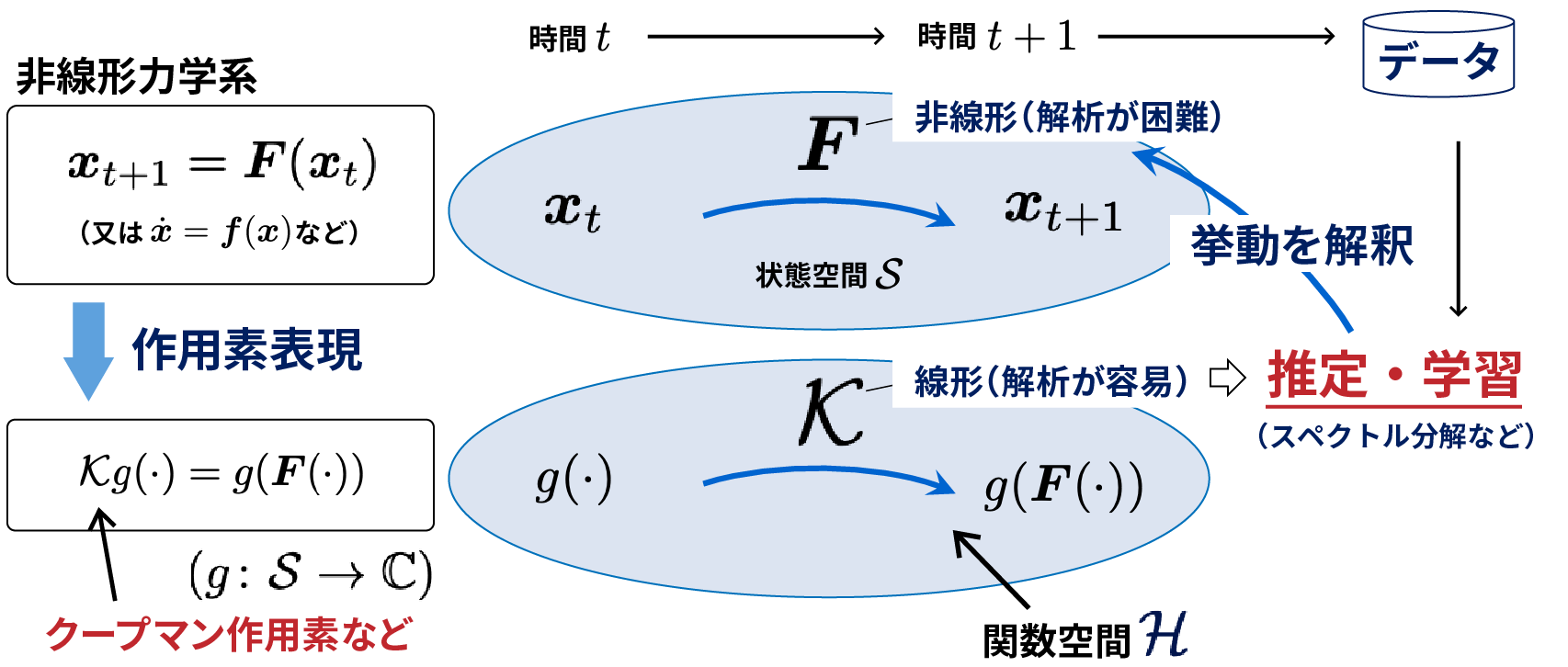
他方、一部の応用数理や物理分野（特に流体力学分野）では近年、作用素論的解析、特にクープマン作用素を用いた一連のダイナミクス解析法が大きく注目されています。この枠組みは、（一般に非線形な）系の時間発展を作用素表現して（関数空間などの）線形領域で扱うことにより、数理的に直接扱うことが困難である非線形性を回避して系の普遍的な動的特性の解析を行います。この枠組みの大きな特徴は、数理モデルを構成する関数系に依らない点にあり、各分野で扱われる現象に対して横断的に適用可能な点にあります。また特に最近では、動的モード分解など、作用素論的解析による解釈が可能なデータを用いた推定法も提案されていて、一定の仮定下で、推定量を種々の物理的特性や原理（縮約モデルなど）と直接結びつけることができるため、多方面の科学分野で適用され学術的にも注目されています。

研究の目的と意義

このような背景から、作用素論的解析とその推定法を、数学・物理的方法による順方向的解析と、機械学習・数理統計的方法による逆方向的解析の両観点から同時的にアプローチして融合化・拡張させて、ドメインで培われてきた数理モデルとデータ駆動による抽出情報をその動力学的特性を介して直接結びつける方法論を構築することが、データからの現象の理解に基づく科学的知見の抽出、しいては複雑現象のより精緻な予測・シミュレーションの実現を可能とする新たな枠組み創出へつながる、と考えました。本研究提案では、このような方針の下、統計的推測による作用素論的解析に基づく複雑現象からの主要ダイナミクス同定法の確立と、その物理的解釈・利用や数理的拡張のための理論構築、およびそれを数理モデルと統合的に用いて知識発見や学習・予測を行うための方法論構築を主な目的として研究を進めます。そして得られた手法や理論的枠組みを、複雑な生体現象や流体現象など、種々の科学分野でのデータ解析へ横断的に適用して実践的に有用性を証明することまでを目標とします。 本研究で創出する計算基盤技術は、多くの科学・工学分野で興味の対象となる動的な複雑現象へ横断的に適用可能で、その学術的波及効果は大きいと考えられます。また、数理モデルと、データ駆動による抽出情報を統合的に用いる汎用的な方法論構築を行う研究であるため、複雑現象に対する精緻なシミュレーション・予測などへ応用可能であり、防災・医療をはじめとした広い社会課題において有用な情報基盤技術の一つとなることが期待されます。

体制と役割

本研究では、このような課題に対して、機械学習・数理統計グループ（河原（九大IMI/理研AIP））、数学グループ（坂内（慶応/理研AIP））、非線形物理グループ（中尾（東工大））、そして生物モデリング・グループ（黒澤（理研iTHEMS））の4グループを構成して取り組みます。機械学習Gはデータ駆動的観点、非線形物理Gは数理モデル的観点から取り組み、数学Gはこれらをつなぐ数学的原理を探求します。そして生物モデリングGは、研究全体を通しての開発手法の適用的検証と方法論・原理へのフィードバックを行います。また特に応用的な研究項目については、参加者のこれまでの共同研究などを軸に、複数分野におけるドメイン研究者との連携に基づき、横断的に開発手法を適用し研究を遂行します。