研究内容

本研究は、主に下記の４課題を解決することで（研究概要）に記載した目標の達成を目指します。

(課題１) 力学系の作用素論的データ解析のための統計的推測法の確立 既存の作用素スペクトル推定法や、河原(代表)らが構築してきた動的モード分解の確率的定式化を更に発展させて、種々の状況に応じた推定法の開発や、統計的に有意な主要ダイナミクスを特定するための方法論の構築を行います。

(課題２) 連続スペクトルを持つ系への拡張のための数理体系の構築 連続スペクトルを持つ系の解析法の開発は複雑現象を扱うために不可欠であるが、点スペクトルのみの場合に比べ数理的扱いが困難になるため、幾何学を中心とした厳密な数学的枠組みに基づき綿密な検討が必要となります。ここでは既存の推論方法を連続スペクトルを持つ場合へも適用可能なものへ拡張を行うと同時に、付随する仮定等を明確化し体系化を進めます。そして特に、異なる時空間スケールを持つダイナミクスが相互作用する系や、カオス的現象など、物理的に重要な状況に着目し、得られる推定量と、既存の物理的概念や不変量、数理モデルの縮約との関連について数学的な整備を進めます。

(課題３) 数理モデルと抽出情報を統合的に用いた学習・予測のための計算体系の構築 数理モデルと抽出情報をそれらの動力学的特性を介し相互利用した、予測・学習の体系的な方法論の構築を進めます。例えば、ニューラルネットなどの学習モデルは、階層的な非線形力学系とも捉えられ、最近ではその特性を利用した学習モデルも報告され注目されています。学習モデルの学習・推論において、そのモデルの力学系としての性質を利用しつつ、作用素論的解析により得られる動力学的特性を統合的に用いる学習・推論のための枠組みの構築とその理論解析について取り組みます。

(課題４) 諸科学におけるデータ解析への横断的適用による展開 諸分野における動的な現象に対して、上記3課題で得られる枠組みを横断的に適用して検証を進めます。一つには、上記課題で得られた作用素論的解析とその推定法、および数理的解釈に基づいて、ドメインにおける数理モデルで表現しきれない原理に関する知識抽出のためのデータ解析を行います。また、従来予測が困難であったレアな現象や複雑に要因が連関する現象、またはより精緻な予測が必要となる応用において開発手法を適用してその有用性についても検証します。

まず（課題1）において、作用素論的解析に基づく統計的推測法の確立とその数学的解釈のための体系化を行い作用素論的データ解析の創出と体系化を行います。(課題2)は、これを複雑な現象への適用を実現するための数理的拡張で、科学的に興味のある現象への適用を可能とするために必要となります。(課題3)は、これら課題により得られる方法を、数理モデルと統合的に用いて、複雑現象に対する予測や、学習機構の拡張へ利用する方法論的な展開になります。そして(課題4)では、生物モデリングにおける課題を中心として、複数ドメインにおける動的機構の解析が重要となる課題へ開発手法を横断的に適用しその有用性を検証します。

研究の意義

本研究の成果により直接的に得られる、科学技術イノベーション創出の観点からの科学技術上の主なインパクトは、学術的独自性と意義を鑑みて次の3点であると考えます。

1. 分野横断的な新たな科学へのアプローチのための方法論とその理論体系の構築を行う提案である点
一般にこれまでの科学研究では、散発的なものを除き、基本的には分野毎に数理モデルが構築され縦割りで研究が進んできました。本研究で開発する枠組みは、非線形力学系の作用素表現とその統計的推定という汎用的な数理的原理に基づきます。そのため、構築される方法論は、多くの分野で共通して興味の対象である動的な複雑現象に関して、各ドメインの数理モデルと計測データがあれば分野横断的に適用可能なもので、これにより得られる抽出情報は開発する理論体系により各ドメインの知識と関連付けることができます。そのように本研究の成果は、提案内で検証を予定しているドメインに限らず、広く他の科学・工学分野への波及が期待されます。

2. 動力学的特性を介してデータ駆動による抽出情報を数理モデルと統合的に用いる枠組み創出を行う点
防災や医療（生命現象の予測）など社会的に重要な課題では、レアな現象や、多スケールが連関する現象などの複雑な状況においても精緻な予測・シミュレーションが求められます。本研究で開発する枠組みは、上記のような数理的原理に基づくため、データの生成機構の動力学的特性を介して、数理モデル的解釈が可能な（つまり動的現象の原理的メカニズムに関する）情報抽出を行うものです．そのため、各ドメインにおける原理に直結する科学的知見の獲得のみならず、数理モデルとの統合的利用による（外挿的な）推論に基づいて、複雑現象のより精緻な予測・シミュレーションの実現が期待できます。

3. 厳密な数学的原理に基づくデータ解析の方法論構築と体系化を行う点
本研究では、現象メカニズムの物理的解釈に直接結びつくデータ解析の構築を目的とするため、データを生成する非線形力学系の数学的性質を厳密に調べることが重要となります。そのため本研究では、多分野にわたる数学研究者が参加し、直接的に関係のある力学系の理論や、背景に現れる関数解析・作用素環論の理論をはじめ、幅広い数学分野の手法をこの課題に応用します。本研究では、このような数学的に厳密な議論の上にデータ解析の枠組み構築を行うため、上記の2点をより確かな、かつ汎用性の高いものにすると言えます。

研究体制と各グループの役割

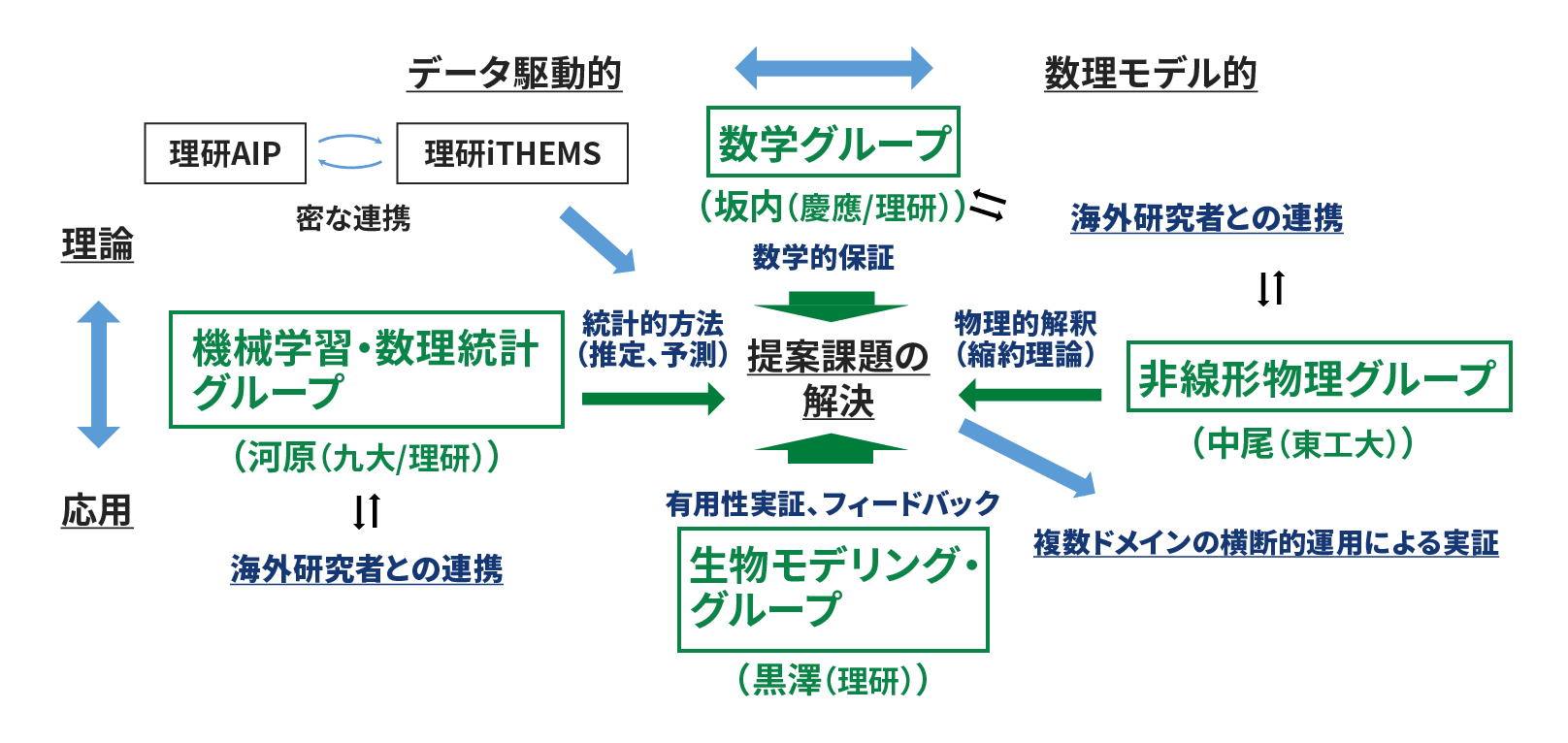
本研究では、このような課題に対して、機械学習・数理統計グループ（河原（九大IMI/理研AIP））、数学グループ（坂内（慶応/理研AIP））、非線形物理グループ（中尾（東工大））、そして生物モデリング・グループ（黒澤（理研iTHEMS））の4グループを構成して取り組みます。機械学習Gはデータ駆動的観点、非線形物理Gは数理モデル的観点から取り組み、数学Gはこれらをつなぐ数学的原理を探求します。そして生物モデリングGは、研究全体を通しての開発手法の適用的検証と方法論・原理へのフィードバックを行います。また特に応用的な研究項目については、参加者のこれまでの共同研究などを軸に、複数分野におけるドメイン研究者との連携に基づき、横断的に開発手法を適用し研究を遂行します。